Um fio cilíndrico de raio transporta uma corrente uniformemente distribuída por sua seção reta e com sentido saindo do papel.
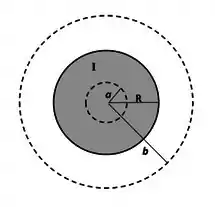
Encontre os raios das espiras amperianas circulares centradas no eixo do fio para as quais o campo magnético gerado pelo fio é dado por:
Passo 1
Para determinar os raios das amperianas, precisamos, obviamente usar a lei de Ampère, ela diz o seguinte:
Nossa curva será um círculo, pela simetria, temos que o campo magnético(dado pela regra da mão direita), será sempre paralelo ao vetor , e será sempre constante, temos então:
Passo 2
Vamos começar calculando o raio !
Para esse raio, a corrente interna não vai ser a corrente total, precisamos determinar a corrente por unidade de área é dada, se liga!
Para , a corrente interna à amperiana fica:
Agora é só substituir os valores na Lei de Ampére e correr para o abraço!
Belezinha! Para determinar , fica mais fácil ainda, porque a corrente interna é , se liga no próximo passo!
Passo 3
Para esse raio, a corrente interna será , substituindo os valores na Lei de Ampére temos:
Resposta
;