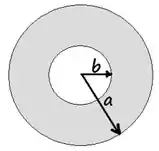
A figura abaixo mostra a seção reta de um condutor cilíndrico concêntrico oco, infinitamente longo, de raio externo e raio interno , carregando uma corrente total . Supondo que a densidade de corrente seja homogênea por todo condutor. A intensidade do campo magnético fora do condutor , dentro do condutor e fora do condutor valem respectivamente:
a)
b)
c)
d)
e)
Passo 1
Como de costume, vamos fazer o problema de lei de Ampère de dentro para fora OK? Primeira coisa: dentro do condutor, a amperiana não vai envolver corrente nenhuma. Por isso, o campo magnético lá dentro é igual à zero. Ou seja em .
Passo 2
Dentro do condutor, a gente imagina uma superfície cilíndrica com raio entre 𝑏 e . A amperiana não vai envolver toda a corrente, só parte dela:
E para calcular essa densidade , como a corrente se distribui uniformemente, é só a gente dividir a corrente total pela área total:
E aí, substituindo:
Passo 3
Agora é pegar o resultado do segundo passo e substituir na lei de Ampère:
Para .
Passo 4
Já para corrente de fora () a coisa fica mais tranquila: a corrente envolvida é o próprio :
Resposta
Letra (D).