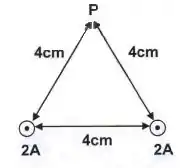
Dois fios retos longos perpendiculares ao plano do papel estão nos vértices de um triângulo equilátero, como mostra a figura. Cada um deles conduz uma corrente de para fora do papel. O campo magnético no terceiro vértice em uma magnitude (em Tesla):
(a)
(b)
(c)
(d)
(e)
Passo 1
O campo magnético gerado por cada um dos fios é perpendicular à linha que liga este fio ao ponto P.
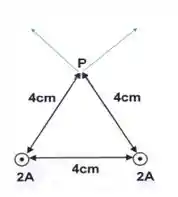
Como os dois fios têm a mesma corrente e estão a mesma distância do ponto , então os campos produzidos por cada fio terão a mesma intensidade.
Passo 2
Desenhando os ângulos dessa figura, em baixo dá pra ver que temos um triângulo equilátero, assim o ângulo de baixo é de . Como os vetores de campo magnético fazem com as linhas que ligam as correntes até o ponto , o ângulo de cima é o que falta pra completar , ou seja,
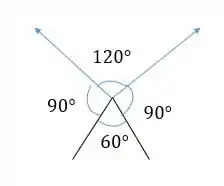
Traçando uma reta vertical
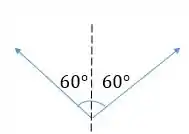
Olhando pra figura, as componentes horizontais de cada um dos campos irão se cancelar, enquanto que as componentes verticais se somam!
O campo resultante é, então:
Ou seja, 2 vezes (por que são dois campos) a componente vertical do campo.
Pela lei de Ampère o campo produzido por um fio infinito é calculado pela circulação do campo magnético
Tomando como amperiana um círculo de raio centrado em um dos fios
Substituindo na equação anterior
Resposta
(a)