UFRJ – Física 3 – 2020.2 – PF – M.Escolha
Uma placa condutora infinita de espessura é posicionada de forma que seu plano médio coincide com o plano de um sistema de coordenadas, como mostrado na figura abaixo. Ela possui uma densidade de corrente constante dada por . Nessa situação, o campo magnético produzido pela placa nas regiões e vale, respectivamente:
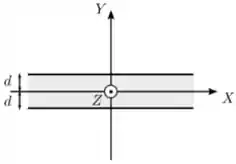
Escolha uma:
e
e
e
e
e
e
e
e
Passo 1
Vem comigo que a gente resolve essa, juntos!
Para encontrar a direção do campo magnético podemos usar a regra da mão direita, apontando o polegar para a direção da corrente, que no caso vai ser a mesma direção de , e a direção que os outros dedos fecham é a direção do campo magnético.
O módulo do campo do campo magnético de uma placa infinita condutora é dado por:
Então precisamos relacionar a corrente com a densidade de corrente , como essa densidade é constante em toda a placa, temos que:
Vem comigo!
Passo 2
Então nosso módulo do campo fica da seguinte forma:
Passo 3
Agora vamos achar o sentido do campo em cada região.
Pela regra da mão direita o campo magnético vai ter sentido anti-horário, logo na região ele vai apontar para e na região ele vai apontar para , assim:
Para :
Para :
Então a nossa alternativa vai ser a letra .
Resposta
e