Um capacitor de placas planas paralelas, circulares e cujo raio das placas é muito maior que a distância entre as mesmas está inicialmente descarregado. A partir de um certo instante, o capacitor começa a ser carregado por uma corrente que cresce linearmente com o tempo , onde . Sobre os campos elétrico e magnético que podem eventualmente surgir entre as placas durante o carregamento do capacitor, pode-se afirmar que:
- Surgirá apenas um campo elétrico estacionário
- Surgirão um campo elétrico estacionário e um campo magnético não estacionário, colineares entre si
- Surgirá apenas um campo elétrico não estacionário.
- Surgirão um campo elétrico não estacionário e um campo magnético estacionário, colineares entre si
- Surgirão um campo elétrico não estacionário e um campo magnético estacionário, perpendiculares entre si
- Surgirão um campo elétrico e um campo magnético, ambos não estacionários, e perpendiculares entre si
Passo 1
Capacitor sendo carregado é tratado sempre pela Lei de Ampère corrigida:
Fazendo uma Amperiana circular e perpendicular, paralela às placas do capacitor e dentro da região entre elas:
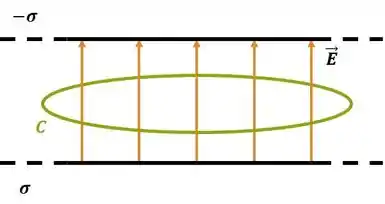
Passo 2
Entre as placas não existe corrente de condução:
Portanto:
O campo elétrico aponta de uma placa para outra como já sabemos e, para essa equação acima fazer sentido, o campo magnético deve ter um aspecto circular, ou seja, tangente à nossa Amperiana em todos os pontos. Ou seja, surgem dois campos ortogonais entre si.
Passo 3
Agora precisamos determinar se eles variam com o tempo ou não. Como a corrente elétrica varia com o tempo:
Sabemos que a corrente considerada é a de deslocamento, portanto:
Segue:
Podemos ver que o campo magnético varia com o tempo. Se você quisesse podia resolver com todos aqueles argumentos que sempre usamos:
E provar que varia com o tempo pra valer. Mas como é múltipla escolha basta você perceber este fato.
Passo 4
Agora para o campo elétrico novamente temos a equação da corrente de deslocamento:
Isolando e integrando:
Seguindo a definição de fluxo, temos uma espécie de Lei de Gauss:
E dá pra ver que o campo varia já... Mas se você quisesse podia resolver com argumentos idênticos à da Lei de Gauss mesmo:
E provar que varia com o tempo de fato.
Resposta
Letra f