Considere uma espira retangular de lados e () e um fio retilíneo infinito, coplanar. Sabendo-se que o fio retilíneo é paralelo aos lados longos da espira e que o fio e a espira portam, respectivamente, correntes para a direita e e no sentido horário, assinale a única opção incorreta.
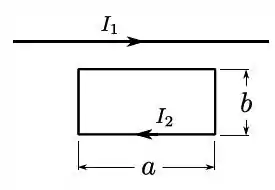
- A soma das forças nos lados curtos da espira é nula;
- A força em cada um dos lados curtos da espira é nula;
- A soma das forças nos lados longos da espira é não nula;
- As forças sobre os lados longos da espira estão na mesma direção;
- A força total sobre a espira é perpendicular ao fio retilíneo.
Passo 1
Como as opções querem saber das forças, vamos fazendo a maldita conta:
O campo do fio retilíneo sai rapidinho por Ampère:
Passo 2
Como o campo gira em torno do fio, colocamos nosso polegar alinhado à ele e temos que o campo entra no plano do retângulo. Agora é moleza, fazemos o produto vetorial para os quatro casos:
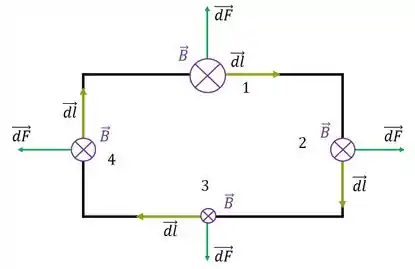
E temos que o campo diminui com a distância, logo:
Ao passo que os campos dos fios verticais se cancelam. Portanto sabemos que a força resultante é algo no sentido de baixo pra cima. Arbitremos como esse sentido:
Passo 3
Agora vamos analisando as afirmativas uma por uma:
Letra a: “A soma das forças nos lados curtos da espira é nula.”
Certa resposta, como já pudemos analisar. Entretanto, cuidado, ele quer a alternativa incorreta! Continuando com nossa análise...
Passo 4
Letra b: “A força em cada um dos lados curtos da espira é nula”
Falsa. Como pudemos observar, a força em cada um desses lados tem um módulo igual a:
Encerrou a questão? Sim, mas para efeito didático, vamos analisando as outras afirmativas...
Passo 5
Letra c: “A soma das forças nos lados longos da espira é não nula;”
Corretíssimo. Como já havíamos analisado, o campo no segmento é menor que o do segmento por conta da distância maior. Logo, apesar das forças terem sentidos opostos, elas não conseguem se cancelar:
Passo 6
Letra d: “As forças sobre os lados longos da espira estão na mesma direção;”
Verdade. Como nós já vimos, elas estão na mesma direção, só não estão no mesmo sentido.
Passo 7
Letra e: ”A força total sobre a espira é perpendicular ao fio retilíneo.”
Sim, nós também já analisamos isto. A força resultante fica no sentido que nós arbitramos como , que é perpendicular ao fio.
Resposta
Letra b.