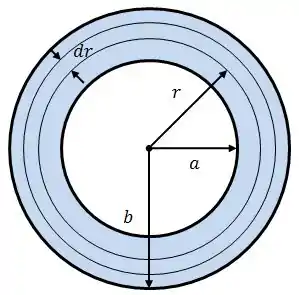
A figura abaixo representa a seção transversal de uma casca cilíndrica muito longa, com raio interno e raio externo . No interior desta casca cilíndrica, existe uma corrente axial . A derivada da corrente elétrica com respeito ao raio é dada pela função .
Calcule a intensidade do campo magnético em função do raio quando .
Calcule a expressão da corrente elétrica em função de .
Calcule a expressão da intensidade do campo magnético em função do raio quando .
Passo 1
Calcule a intensidade do campo magnético em função do raio quando .
O campo magnético é determinado a partir da lei de Ampère, que é dada por:
Onde é a corrente englobada pela amperiana.
Utilizando a simetria do problema, a amperiana será um círculo de raio , a expressão de lei de Ampère pode ser simplificada para:
Entretanto, na região não existe nenhuma corrente, logo:
Passo 2
Calcule a expressão da corrente elétrica em função de .
O enunciado nos disse que, para (que é onde tem corrente):
Então, para calcular a expressão de , basta integrar esse cara:
Obs.: Temos que integrar esse cara de até porque nas regiões e , a corrente é nula.
Passo 3
Calcule a expressão da intensidade do campo magnético em função do raio quando .
Aqui, novamente, vamos ter que usar a lei de Ampère:
Fazendo as mesmas simplificações que usamos na letra , teremos:
A diferença aqui é que, para a região , a corrente interna é dada por:
Substituindo isso na expressão de , teremos:
Resposta