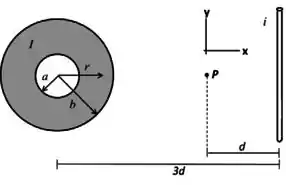
A figura mostra a seção transversal de uma casca cilíndrica muito longa de raio interno e raio externo , que conduz uma corrente uniformemente distribuída. O fio mostrado à direita só será usado no item .
Utilizando a Lei de Ampère, calcule o módulo do vetor magnético a uma distância do centro para .
Conforme mostra a figura, a casca cilíndrica está paralela ao eixo e um fio retilíneo muito longo, que transporta uma corrente , está paralelo ao eixo . O campo magnético resultante destes dois objetos é medido fora da casca cilíndrica no ponto , e vale: . Sabendo que , encontre as intensidades das correntes (na casca) e (no fio) e seus respectivos sentidos (forneça as respostas em termos dos vetores unitários)
Sugestão: o módulo do vetor campo magnético de uma distribuição cilíndrica muito longa, que transporta uma corrente , à distância , vale:
Passo 1
Utilizando a Lei de Ampère, calcule o módulo do vetor magnético a uma distância do centro para .
Já tá na cara que vamos ter que suar com a Lei de Ampère, certo?
Como se trata de uma geometria cilíndrica, a nossa amperiana será uma circunferência de raio , onde . Portanto:
Então o nosso trabalho aqui é descobrir quanto vale a corrente interna.
Como o problema disse que a corrente está uniformemente distribuída, podemos simplesmente fazer uma regra de três pra descobrir a corrente interna.
Portanto, o módulo do campo magnético será:
Passo 2
Conforme mostra a figura, a casca cilíndrica está paralela ao eixo e um fio retilíneo muito longo, que transporta uma corrente , está paralelo ao eixo . O campo magnético resultante destes dois objetos é medido fora da casca cilíndrica no ponto , e vale: . Sabendo que , encontre as intensidades das correntes (na casca) e (no fio) e seus respectivos sentidos (forneça as respostas em termos dos vetores unitários)
Sugestão: o módulo do vetor campo magnético de uma distribuição cilíndrica muito longa, que transporta uma corrente , à distância , vale:
Bom, beleza! O problema já nos disse que o campo magnético no ponto possui duas componentes.
Utilizando a regra da mão direita, a casca cilíndrica vai gerar um campo magnético, no ponto , na direção . E o fio condutor vai gerar, no ponto , um campo magnético na direção .
Para que a componente seja positiva, a casca cilíndrica deve conduzir a corrente no sentido saindo da página. Da mesma forma, para que a componente seja negativa, a corrente deve estar no sentido , de cima para baixo.
Para descobrir o valor de cada corrente, basta trabalhar com cada componente do campo magnético resultante no ponto .
Passo 3
Já vimos que a casca cilíndrica será a responsável pela componente do campo magnético.
De acordo com o a Lei de Ampère, o campo magnético para a casa cilíndrica será:
Para regiões onde . Onde Logo:
Passo 4
Vimos também que o fio condutor será responsável pela componente do campo magnético.
Para o fio condutor, o problema mesmo já quebrou o nosso galho.
Onde . Logo:
Resposta