Considere um fio cilíndrico circular, sólido, de raio e com altura infinita, como mostrado na figura abaixo. Através de tal fio, há uma densidade de corrente elétrica estacionária, mas não uniforme dada por , onde é uma constante positiva, é a distância até o eixo do fio e o seu correspondente unitário.
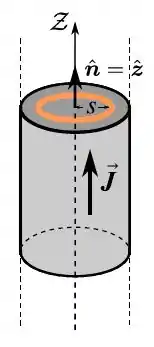
(a) Determine a intensidade de corrente elétrica que passa através de uma seção transversal qualquer do fio. Sugestão: tome como elemento de superfície um anel de raio e espessura infinitesimal .
(b) Sendo um ponto arbitrário com coordenadas cilíndricas , informe qual(is) componente(s) do vetor campo magnético é (são) nula(s), indicando ainda de que coordenada(s) ela(s), de fato, pode(m) depender. Justifique.
(c) Com base no resultado do item (b), identifique uma curva fechada e orientada apropriada para a dedução do campo magnético, e determine uma expressão para a circulação de tal campo ao longo dela:
(d) Aplicando a lei de Ampère, deduza expressões para o vetor campo magnético (i) fora
e (ii) dentro do fio.
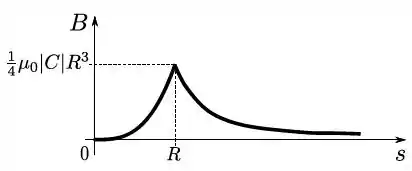
(e) Faça um esboço cuidadoso do gráfico do módulo de como funções de , marcando explicitamente
quaisquer pontos relevantes.
Passo 1
Se liga! A expressão para a densidade de corrente é dada por
Podemos ver que ela não é dependente de .
Sendo a corrente elétrica
Como a densidade independe de , podemos escolher uma seção transversal para calcular a corrente
Se tomarmos na mesma direção de e um anel de raio e espessura , podemos escrever que
Substituindo essas informações
Opa! Já acabamos de resolver o item (a).
Passo 2
No item (b), o vetor campo magnético é escrito como
E queremos saber qual(is) componentes são nulas.
Aqui devemos lembrar da lei de Gauss do magnetismo.
Considerando a simetria cilíndrica, podemos tomar um cilindro fechado de raio .
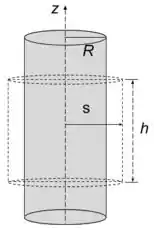
Aplicando a Lei de Gauss para as tampas inferior e superior e a borda temos.
Considerando que as partes correspondentes a contribuição da parte inferior e superior se cancelam, temos
Isto implica que
Como a orientação da corrente do cilindro está no eixo , temos que haverá um campo ao redor deste cilindro. Sendo assim, podemos dizer que existirá campo na direção de . Portanto
Passo 3
No item (c), queremos a circulação. Sendo assim, queremos
Como já sabemos que só há campo é constante na direção , e que o campo está em torno do nosso cilindro descrevendo uma circunferência, temos
Só precisamos lembrar do comprimento da circunferência.
Passo 4
No item (d), queremos a campo dentro e fora do fio.
Fora do fio devemos levar em consideração a corrente total, já calculada anteriormente
Pela Lei de Ampère
Para dentro a corrente é dada por
Agora vamos aplicar a Lei de Ampère
Passo 5
No item (e), precisamos montar um gráfico para o campo. Para isso podemos usar as informações do campo dentro e fora calculadas no item (d).
Repare que na parte de dentro o campo cresce com a distância e na parte externa decai com . Daí temos o gráfico