
A)
B)
C)
D)
E)
Passo 1
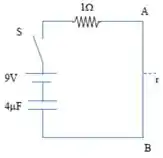
A coisa mais importante dessa questão é entender que o capacitor não pode sofrer variações bruscas de potencial mas a corrente nele pode mudar e sofrer saltos.
Quando a gente fecha a chave , o capacitor continua com o seu potencial igual a nos primeiros segundos depois desse fechamento.
Então, de início, a corrente que passa em é igual a:
Passo 2
Quando o capacitor fica totalmente carregado, uma DDP de surge em cima dele, com orientação oposta ao potencial da bateria.
Quando isso acontece, a corrente cai para zero, pois o capacitor fica saturado e não dá mais para entrar cargas nele.
Aí, a corrente que passa em , nessa situação, vale . Aqui a gente já pode eliminar de cara as alternativas (B) e (C). Afinal, sem corrente, sem campo magnético!.
Passo 3
Mas precisamos voltar para o passo a profundar um pouquinho para achar a resposta certa. Pela lei de Ampère, dá para descobrir quem é esse campo magnético que a questão pede:
Fizemos uma amperiana circular ao redor do fio e com raio
Agora é só substituir:
Resposta
Letra (A)