Considere o cabo coaxial muito longo da figura abaixo, formado por um cilindro central de raio e uma casca cilíndrica externa de raios e , concêntrica com cilindro.
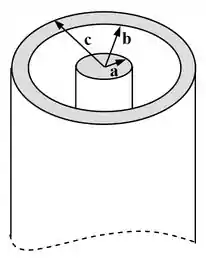
Sabendo que uma corrente flui no cilindro e uma corrente flui na casca cilíndrica (em sentidos opostos):
Calcule o campo magnético (módulo, direção e sentido) em todas as regiões do espaço considerando que as corrente estão uniformemente distribuídas nas seções transversais do cilindro e da casca cilíndrica.
Faça um gráfico do módulo de em função do raio (distância ao centro do cabo).
Passo 1
Para determinar o campo magnético em todas as regiões, vamos usar a lei de Ampère, ela diz o seguinte:
Nossa curva será um círculo, pela simetria, temos que o campo magnético(dado pela regra da mão direita), será sempre paralelo ao vetor , e será sempre constante, temos então:
Vamos ver como fica o campo para as diferentes regiões:
- :
- :
Para essa região, a corrente interna vai variar para cada valor de , por isso precisamos determinar a corrente para cada valor de ! A corrente por unidade de área é dada por:
Para diferentes valores de , a corrente fica:
Agora é só jogar na lei de Ampère!
Passo 2
Para essa região, temos que a corrente interna será toda a corrente que passa no cilindro central, a Lei de Ampère fica assim:
Passo 3
Para essa região, devemos fazer o mesmo mimimi da região , pois a corrente interna vai variar com , temos então que a corrente por unidade de área é dada por:
Para diferentes valores de , a corrente interna fica:
Vamos agora aplicar a Lei de Ampère, mas lembre-se, não podemos esquecer da corrente que passa pelo cilindro central, a corrente interna à Amperiana será:
Agora sim, vamos aplicar a Lei de Ampère:
Passo 4
Para essa região, temos que a soma das correntes internas , portanto:
Passo 5
O gráfico do módulo do campo magnético e função do raio deve ser algo assim:

Calculamos o valor do campo para e através das fórmulas!
Resposta
Resposta
Ei, a resposta está no passo a passo :)