Lei de Ampère
Determine a circulação para as três curvas fechadas orientadas respectivamente.
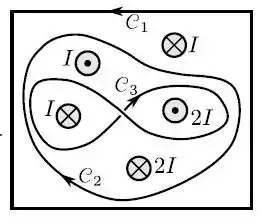
- pois todas são perpendiculares.
Passo 1
Clássica questão de circulação de corrente. Pela regra da mão direita, colocamos nossos dedos alinhados à orientação de cada curva e determinamos os sentidos dos vetores área.
À partir daí sabemos qual corrente é positiva e qual é negativa. Fazendo um por um:
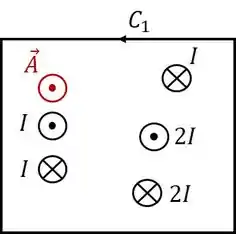
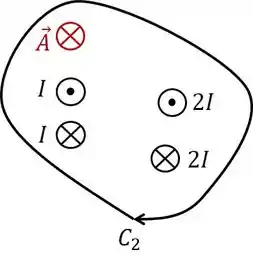
Esse último tem aquela sacanagem de dividir em duas curvas:
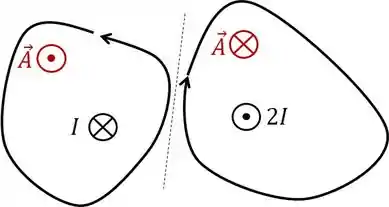
Portanto temos nossa resposta.
Resposta
Letra e
Exercícios de Livros Relacionados
41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo