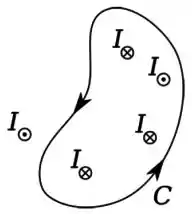
A figura abaixo mostra uma curva fechada, orientada, e um trecho de um fio retilíneo, longo, pelo qual passa uma corrente estacionária de intensidade , no sentido indicado. Podemos afirmar que:

Vamos precisar da lei de Ampère, que diz o seguinte:

ou seja, a circulação do campo magnético (ou a integral de linha de  ao longo da curva fechada ), , é diretamente proporcional à corrente total que atravessa a área definida por essa curva fechada (amperiana).

A primeira coisa importante aqui, então, é que as correntes que contribuem para são aquelas que estão atravessando a área definida pela curva fechada (amperiana) . Com isso, já podemos jogar fora aquela corrente que está do lado de fora de saindo da página porque ela não vai contribuir para a conta.

Depois disso, precisamos determinar, a partir do sentido da amperiana , quais vão ser as correntes positivas e as negativas.

Bom, como curva fechada está no sentido anti-horário, pela regra da mão direita, as correntes positivas vão ser aquelas que estão saindo da página e as negativas serão aquelas que estão entrando, beleza?

Por isso, a corrente que atravessa a área definida por é:

Para fechar, jogando isso na lei de Ampère, temos