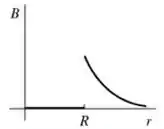
Um cilindro condutor, muito longo, oco, de paredes finas (como um tubo) de raio carrega uma corrente uniformemente distribuída ao longo do seu comprimento. Qual dos gráficos abaixo descreve mais precisamente a magnitude do campo magnético produzido por esta corrente como uma função da distância ao centro do cilindro?
Passo 1
Como o cilindro é oco, não há corrente no seu interior e, portanto, de acordo com a Lei de Ampère, para .
Passo 2
Para , temos:
Aqui consideramos que:
- A curva fechada de integração é um círculo concêntrico ao cilindro de raio ; e
- A corrente que circula pelo cilindro é .
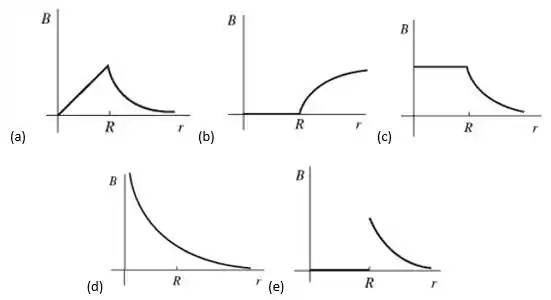
Bem, a partir da expressão acima, percebemos que e, portanto, seu gráfico é decrescente e sua concavidade é voltada para cima (para , como no item (e).
Resposta
(e)
Exercícios de Livros Relacionados
41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo