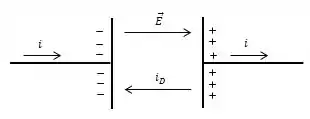
Um capacitor é construído com duas placas circulares de raio , colocadas a uma distância de uma da outra. Este capacitor é inicialmente carregado. Num determinado instante, passa por ele uma corrente de no sentido mostrado pela figura.
- Indique, numa figura desenhada na folha resposta, o sentido do campo elétrico no interior do capacitor e o sentido da corrente de deslocamento.
- Calcule o campo magnético gerado a uma distância de do eixo de simetria do capacitor na região entre as placas.
- Calcule o campo magnético gerado a uma distância de do eixo de simetria do capacitor na região entre as placas.
Justifique todas as suas respostas.
Passo 1
Como já sabemos, campo elétrico vai da carga positiva para a carga negativa e a corrente de descolamento tem o mesmo sentido da corrente do circuito, logo:
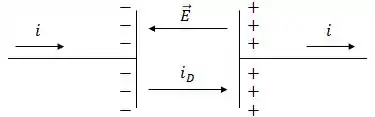
Passo 2
Perceba que significa que o ponto escolhido está fora da região entre as placas do capacitor, fazendo com que a amperiana envolva toda a corrente de deslocamento. Como queremos achar o campo magnético , aplicamos a lei de Ampère:
Isolando o campo magnético,
Agora é só substituir os valores.
Considere .
Passo 3
Neste caso da distância , a amperiana não engloba toda a corrente de deslocamento. Faremos, assim, uma razão entre as áreas para encontrarmos a corrente a ser considerada nos cálculos.
A princípio, continuaremos com a fórmula
Mas precisaremos calcular o novo , o qual chamaremos de , levando em consideração o raio da amperiana que chamaremos de .
Agora, só substituir na fórmula do campo magnético: