Considere a espira quadrada de lado da figura abaixo, percorrida por uma corrente de intensidade constante no sentido horário. O sistema de coordenadas está indicado na figura, com o semieixo positivo-z saindo do plano do papel em direção ao leitor. Lembre-se que .
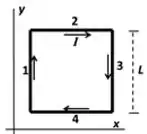
- Em toda a região da espira existe um campo magnético externo homogêneo dado por . Qual (ou quais) dos segmentos de fio, numerados na figura, não sofrem força magnética devida ao campo externo? Justifique.
- Calcule, em relação ao centro da espira, o vetor torque resultante devido ao campo externo nas condições do item (a)
- Desconsidere agora o campo externo e suponha que os fios e tenham comprimento de apenas . Deste modo, os fios e podem ser considerados “muito longos”, paralelos e separados pela distância de . A corrente na espira continua com intensidade . Encontre o módulo da força que o fio 1 exerce numa seção de 2,0 cm do fio 3 afastada de suas extremidades e responda se essa força é de atração ou repulsão.
- Sabendo que , encontre o valor da nova corrente que percorre a espira quadrada e informe também o seu sentido (horário ou anti-horário)
Considere agora a próxima figura, em que a linha amperiana aparece envolvendo os fios e da espira quadrada analisada anteriormente.
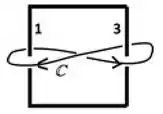
Passo 1
Temos que a força magnética é dada por
Quando a velocidade e o campo magnético são paralelos, temos que o produto vetorial acima é nulo e consequentemente a força também.
Como o campo magnético está na direção , em todos os fios que tivermos corrente nessa direção a força magnética será nula.
Assim temos que nos fios e a força magnética é nula!
Passo 2
O vetor torque resultante é dado por
O vetor momento magnético é dado por
(O sinal de menos, vem do fato da corrente está no sentido horário, ou seja, pela regra da mão direita o vetor está entrando na página)
Assim o torque é dado por
Passo 3
Pegando esse limite de fio infinito, o fio produzirá um campo magnético que podemos calcular pela lei de Ampére
Pela regra da mão direita esse campo produzido está na direção quando sobre o fio .
Dessa forma a força sobre um infinitésimo do fio é dada por
Como a corrente no fio está na direção , temos
E a força total será dada por
Onde é a seção de comprimento que o enunciado pede. Substituindo o campo magnético temos
E por aqui já vemos que a força entre os fios é repulsiva (aponta na direção positiva de , afastando do fio ).
Assim
Passo 4
Aqui temos que prestar atenção na orientação na nossa linha amperiana!
Do lado direito, usando a regra da mão direita, definimos correntes positivas aquelas que passam por essa região e apontam para cima. Da mesma maneira, do lado esquerdo definimos correntes positivas aquelas que passam por essa região apontando para baixo.
Pela lei de Ampére, temos
Como essa circulação, dada pelo enunciado, é positiva temos que no lado direito a corrente vai para cima e do lado direito ela vai para baixo, de forma que na espira a corrente está no sentido horário.
Como a corrente na espira, passa duas vezes por essa amperiana temos que
Como
Resposta
(a) e , já que o campo é paralelo à corrente
(b)
(c) , repulsão
(d) , horário