Um cilindro condutor muito comprido, com o seu eixo orientado ao longo do eixo , transporta uma corrente elétrica cuja densidade é . A densidade de corrente, definida como a corrente por unidade de área, é simétrica em relação ao eixo do cilindro, mas não é uniforme e varia radialmente de acordo com a seguinte relação:

Onde “” é o raio do cilindro, “” é a distância radial entre o ponto considerado e o eixo do cilindro e “” é uma constante com unidades [].

a) Calcule o valor da corrente total que passa através da seção reta do fio.

b) Utilizando a Lei de Ampère, calcule o módulo do campo magnético na região.

c) Obtenha a expressão para a corrente contida em uma seção reta circular de raio , centralizada no eixo do cilindro.

d) Utilizando a Lei de Ampère, calcule o módulo do campo magnético na região .

e) Como se comparam os resultados dos itens b) e d) quando ?

b)

Agora temos que calcular o módulo do campo magnético na região fora do fio, usando a lei de Àmpere.

A lei de Àmpere é essa daqui:

Lembrando que estamos integrando sobre a curva amperiana, e que é toda a corrente que está dentro dessa curva.

Como queremos o campo na região fora do fio, vamos escolher uma amperiana que esteja por fora do fio:

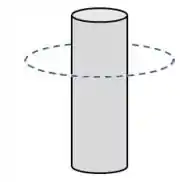
A curva amperiana é o círculo tracejado de raio .

Notem que a corrente que está dentro da amperiana é toda a corrente, , como já vimos na letra a).

Então

Pois tanto o campo magnético como o elemento infinitesimal da curva estão “girando” ao redor do fio, então eles são paralelos a cada ponto.

O módulo de é constante ao longo de uma amperiana, pois ele estará sempre a uma distância do fio.

Então

Então, para fora do fio, na região em que , o módulo do campo vale:

c)

Aqui é parecido ao que fizemos na letra a), mas agora não queremos a corrente total. Queremos saber qual é a corrente que está contida em uma seção circular de raio , tal que . Dessa vez, vamos deixar a reposta em termos desse raio . Então:

Note que, se fizermos , retornamos para a situação do item a). Que seria a corrente total na seção transversal.

d)

Aqui é parecido ao que fizemos na letra b), mas agora não queremos que a amperiana esteja fora do fio. A nossa amperiana vai ser uma circunferência de raio , e a corrente que ela vai estar envolvendo vai ser , que encontramos na letra c).

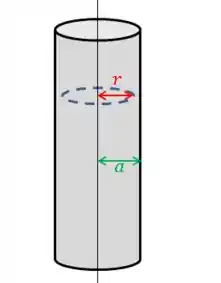
Como já vimos na letra b, e são paralelos ponto a ponto, pois ambos apontam na mesma direção, ao redor do fio. E como o campo é constante sobre a amperiana, podemos tirá-lo da integral e ficamos com:

Substituindo a corrente:

Prontinho!!

e)

no item b) obtivemos:

Quando

No item d), obtivemos:

Quando

Opa! Os resultados são iguais! O que era de se esperar, no ponto em que estamos em cima do fio o campo tem que o mesmo!