Na figura vemos quatro amperianas circulares concêntricas com um fio cuja corrente é dirigida para fora do papel.
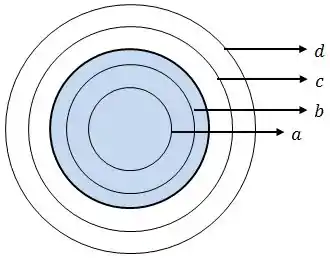
A corrente é uniforme em toda a seção reta do fio (região azulada). Colocando as amperianas na ordem decrescente do valor absoluto de ao longo da curva, obtemos:
;
e empatados, , ;
, , ;
é impossível ordenar sem saber o valor da corrente;
e empatados, , ;
Passo 1
Opa! Quando a questão pede para calcularmos o valor de , já vem a serenidade no olhar de quem sabe que o 10 já é realidade.
Essa integral, também chamada de “circulação de campo magnético” é calculada pela Lei de Ampère.
Onde corresponde à corrente que passa por dentro da amperiana.
Então agora basta analisar cada uma delas, beleza?
Passo 2
- Amperiana :
- Amperiana :
- Amperiana :
- Amperiana :
Vamos chamar de a corrente total que passa pelo fio, e de o raio do fio.
A amperiana aqui está englobando somente parte da seção transversal do fio.
Como a corrente está uniformemente distribuída, a densidade de corrente será constante, logo, podemos calcular a corrente que passa pela amperiana de raio da seguinte forma:
Logo, para a amperiana :
Assim como a amperiana , a amperiana está englobando somente parte da seção transversal do fio.
Dessa forma, fazendo os mesmos cálculos que fizemos anteriormente, teremos:
Já a amperiana engloba todo o fio, dessa forma:
Logo:
Assim como a amperiana , a amperiana engloba todo o fio, dessa forma:
Logo:
Finalmente, organizando os valores de , sabendo que , teremos:
Assim, em ordem decrescente: c e empatados, , ;
Resposta
e empatados, , ;