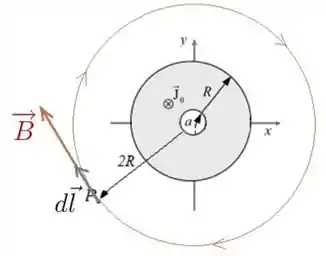
A figura abaixo mostra a seção transversal de um cilindro condutor longo de raio , percorrido por uma corrente de densidade uniforme de módulo e apontando para dentro da página. Nele existe uma cavidade também cilíndrica de raio , centrada com o eixo do cilindro. Considerando-se que o eixo do cilindro é o eixo z, calcule o módulo do vetor campo magnético em um ponto P que está a uma distância do centro do cilindro.
(a)
(a)
(a)
(a)
(a)
Passo 1
Aqui temos que usar a lei de Ampére. Primeiro vamos calcular a circulação do campo magnético, usando o fato de que o campo tem que apontar na direção
Já a corrente total passando pela seção reta do cilindro é dada por
A área da seção reta é a área de uma coroa circular de raio interno e raio externo
Dessa forma
Pela lei de Ampére
Substituindo tudo (e usando )
Resposta
(e)