Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Ampère

Ver Teoria
Exercício 441234567891011121314151617181920212223242526272829303132333435363738394041424345464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

O cabo coaxial mostrado na figura consiste de um cilindro condutor longo e sólido de raio R 1 envolto por um condutor cilíndrico oco de raio R 2 . Os dois conduzem correntes de iguais intensidades I , mas de sentidos opostos.

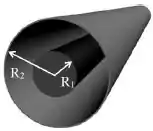
A densidade de corrente é uniforme nos dois condutores. A intensidade do vetor campo magnético nas seguintes regiões r < R 1 , R 1 < r < R 2 , r > R 2 respectivamente são iguais a:

a 0 ,   μ 0 I / ( 2 π R 1 2 )   ,   0

b μ 0 I / ( 2 π R 1 ) ,   μ 0 I / ( 2 π r ) ,   0

c μ 0 I r / ( 2 π R 1 2 ) ,   μ 0 I / ( 2 π r ) ,   0

d 0 ,   μ 0 I / ( 2 π R 1 2 ) ,   μ 0 I /   ( 2 π R 2 )

e μ 0 I r / ( 2 π R 1 2 ) ,   0 ,   μ 0 I / ( 2 π r )

Passo 1

A Lei de Ampère é dada por:

∮ C   B → ∙ d l → = μ 0 I i n t

Aplicando à simetria cilíndrica, temos que:

B r = μ 0 I i n t 2 π r

Agora temos que aplicar a cada caso.

Passo 2

  • r < R 1

    • Como a corrente é uniformemente distribuída, a corrente interna pode ser calculada por uma regra de três:

    I i n t I = π r 2 π R 1 2 → I i n t = I r 2 R 1 2

    Logo:

    B r = μ 0 I r 2 π R 1 2

    Passo 3

  • R 1 < r < R 2

    • Nesse caso, a amperiana envolve todo o fio, logo:

    I i n t = I

    Portanto:

    B r = μ 0 I 2 π r

    Passo 4

  • r > R 2

Agora amperiana envolve os dois condutores, assim, como ambos transportam corrente em sentidos opostos:

I i n t = I - I = 0

B r = 0

A resposta certa é a letra c .

Resposta

c μ 0 I r / ( 2 π R 1 2 ) ,   μ 0 I / ( 2 π r ) ,   0

Exercícios de Livros Relacionados

41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo