1. Determine o vetor campo magnético a uma distância de um fio retilíneo longo percorrido por uma corrente elétrica estacionária de intensidade .
2. Determine o vetor campo magnético no centro de uma espira circular de raio percorrida por uma corrente elétrica estacionária de intensidade .
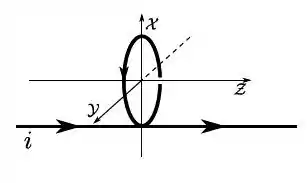
3. A figura mostra um fio retilíneo longo, paralelo ao eixo que é percorrido por uma corrente elétrica estacionária e apresenta uma dobra circular de raio , pertencente ao plano . Sabendo que o fio é recoberto por um esmalte isolante, utilize os resultados obtidos nos itens anteriores para determinar o campo magnético resultante no centro da dobra circular.

Além disso temos que, pela configuração do campo, o módulo deste é constante em toda , portanto:

A integral de pedaços infinitesimais na Amperiana resulta no comprimento desta:

Como se trata de uma circunferência de raio , temos:

Sem falar que a corrente que atravessa a Amperiana é . O vetor campo magnético gira em torno do fio. Arbitremos que o unitário que dá essa direção seja :

Agora vamos determinar o campo magnético no centro de um fio circular. O método mais adequado para este caso é a Lei de Biot-Savart. Enunciando:

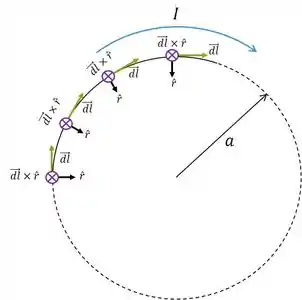
Temos constante e fazemos o produto vetorial para os pontos da circunferência:

Podemos ver que o produto vetorial aponta para dentro da tela em todos os pontos. Pela figura do enunciado, vemos que esse é o sentido de . Logo:

E a integral de é o comprimento do fio.

Portanto temos nosso campo.

Agora o que o enunciado da letra c deseja é simplesmente a soma dos campos no centro da circunferência. Pela regra da mão direita, o sentido do campo feito pelo fio retilíneo no centro é . Como o centro da circunferência dista do fio retilíneo, substituímos na expressão:

Somando com o encontrado na letra b: