USP – Física 3 – 2020 – P-SUB – M.Escolha
. Em uma região cilíndrica de raio , há um campo elétrico homogêneo dado por , onde e são duas constantes e é o tempo.
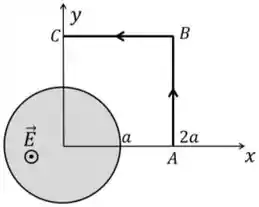
A integral de linha do campo magnético , ao longo do caminho aberto , onde , e é:
. Nenhuma das alternativas
. A integral de linha é zero, pois não á corrente
Passo 1
Vem comigo que a gente resolve essa questão e manda ela embora
Para char o valor da integral pedida no enunciado, vamos usar a lei de Ampère-Maxwell, dada por:
Onde é o fluxo do campo elétrico que passa por uma região delimitada.
Para aplicarmos essa lei precisamos delimitar uma região, reparando na figura o trecho é o mesmo que um quarto de um quadrado de lado , a região fica mais ou menos assim:
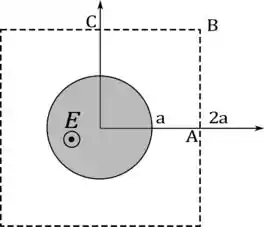
Então vamos aplicar a lei de Ampère-Maxwell nessa região.
Passo 2
Observando a região limitada vemos que não passa corrente nenhuma por ela, logo o segundo termo da lei de Ampère-Maxwell é zero e temos:
O fluxo do campo elétrico é dado por:
Essa área é a área por onde passa o campo elétrico, logo temos que:
Calculando a derivada temporal desse fluxo, temos:
Com isso temos que:
Passo 3
Mas a integral de linha que analisamos é sobre todo o quadrado de lado , mas só estamos interessados na parte que é um quarto desse quadrado, assim temos que:
Com isso vemos que alternativa correta é a letra .