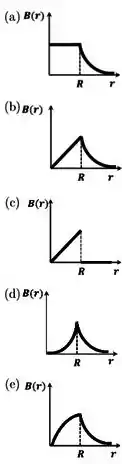
Um cilindro circular maciço, infinito e condutor, de raio , possui uma densidade de corrente estacionária, , onde é uma constante positiva, é a distância ao eixo do cilindro e é um vetor unitário cuja direção é paralela ao eixo do cilindro. Assinale a alternativa cujo gráfico melhor representa o comportamento do módulo do campo magnético produzido pelo cilindro como função da distância .
Passo 1
Temos que, pela regra da mão direita, o campo magnético está na direção . Então fica interessante usar lei de Ampére. Vamos usar como amperiana um círculo de raio centrado no eixo do fio.
A circulação do campo magnético ao longo desse círculo é dado por
Por outro lado, temos que a corrente total passando dentro desse círculo é dada por
Onde e é paralelo à densidade de corrente .
Para uma distância (dentro do fio), temos que a corrente total é dada por
Assim pela lei de Ampére
Ou seja, para , o campo magnético cresce como uma parábola.
Para uma distância (fora do fio), temos que a corrente total vai ser toda a corrente no fio que é dada por
Assim pela lei de Ampére
Ou seja, para , o campo cai como .
O melhor gráfico que representa esse comportamento é o da letra (d)
Resposta
(d)