Halliday - Vol. 3 – 9º edição – Capítulo 29 – Seção 4 – Exercício 44
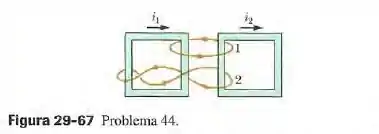
(Capítulo 29.4 – Exercício 44) A figura 29-67 mostra duas curvas fechadas que envolvem duas espiras que ocnduzem correntes e . Determine o valor da integral (a) para a curva 1 e (b) para a curva 2.
Passo 1
Oii pessoal, tudo certinho?
Vamos pra mais uma sobre Lei de Àmpere :P
A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. Ela diz que:
O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fechada, conhecida como amperiana. A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:
onde é a densidade de corrente na curva fechada
Bom, como nesse exercício temos duas curvas fechadas, vamos usar a Lei de Ámpere em cada uma delas, boraa!
Passo 2
Para a curva 1, o resultado da integral será a seguinte:
Passo 3
Já no caso da curva 2, a corrente é contabilizada duas vezes por conta da curva fechada enlaçando a espira 1. Assim:
Fechou??
Resposta
- ;
- .