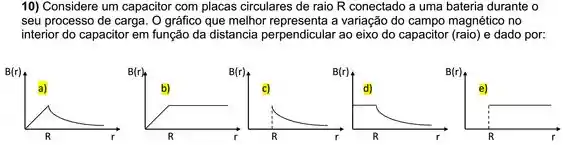
Passo 1
Lembrar da lei de Ampère numa amperiana circular:
Passo 2
Essa corrente interna varia com o raio da amperiana:
1. Se : Nesse caso, somente uma parte da corrente de deslocamento é envolvida. Essa corrente envolvida é proporcional à área envolvida:
Substituindo na lei de Ampère:
Então, até a corrente cresce linearmente.
2. Se : Nessa situação, a corrente interna é a própria corrente total de deslocamento:
Então, substituindo na lei de Ampère:
Nesse caso, a corrente diminui até que seja igual a zero no infinito. Fazendo o esboço dessas duas partes, a gente chega no gráfico da letra (a).
Resposta
Letra (a).
Exercícios de Livros Relacionados
41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo