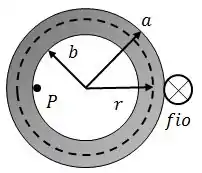
1. Obtenha o módulo do campo magnético para , e para ;

Bom, como queremos calcular o campo magnético, nesse tipo de problema, a boa é sempre ir com a lei de Ampère:

Como o problema aqui tem uma simetria cilíndrica, todas as nossas amperianas (as curvas fechadas que usamos na integração) serão circunferências fechadas, de raio (se trata justamente da linha pontinhada).

Isso significa que podemos reduzir a lei de Ampère para:

O segredo agora é, para cada região, calcular a corrente interna e acabou o problema. Beleza?

Passo 2

Nessa região, não teremos nenhuma corrente dentro da amperiana, logo:

Nesse caso, a ampreriana pega só uma parte da seção reta do cilindro oco. Então, sabendo que a corrente total que passa pelo cilindro é , podemos determinar com uma regra de três:

Substituindo na lei de Ampère:

Essa região engloba todo o fio. Portanto:

E substituindo na lei de Ampère:

Passo 3

• Qual será o módulo de , no ponto , situado em , quando um fio com uma corrente for colocado tangencialmente ao longo do condutor cilíndrico, a uma distância do centro deste?

O campo magnético resultante no ponto será a soma vetorial do campo magnético gerado pelo cilindro com o campo magnético gerado pelo fio .

Para o cilindro, vimos no passo anterior que quando , teremos:

Isso significa que o cilindro não gera campo magnético no ponto , isso significa que o campo magnético resultante será apenas o campo gerado pelo fio:

Sabendo que o fio está a uma distância do ponto , usando a lei de Ampère:

Onde é a corrente que passa pelo fio.

Resposta

a.

b.