A figura abaixo mostra uma região atravessada perpendicularmente por várias correntes estacionárias com intensidades de mesmo módulo . Por convenção, as correntes que saem da página são representadas por ⊙ e as que entram na página por ⊗.
Estão representados, também, três diferentes caminhos fechados, orientados, para a determinação da integral .
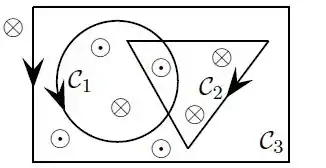
Assinale a opção abaixo que melhor indica a relação entre tais integrais para os diferentes caminhos.
e
e
Não podemos determinar sem conhecermos as dimensões dos caminhos utilizados
Passo 1
Como o problema está pedindo para trabalharmos com a integral , no fundo, ele está implorando para usarmos a lei de Ampère, dada por:
Como aqui não há corrente de deslocamento, podemos simplesmente escrever a lei de Ampère como:
Logo:
Assim, para cada curva, o nosso trabalho é determinar a corrente interna .
Se a curva estiver no sentido anti-horário, as correntes que estiverem saindo da página serão positivas e as correntes que estiverem entrando na página serão negativas.
Se a curva estiver no sentido horário, acontecerá o contrário, as correntes que estiverem saindo da página serão negativas, e as correntes que estiverem entrando na página serão positivas, ok?
Isso fica mais fácil de lembrar se usarmos a regra da mão direita para cada curva.
Passo 2
A curva está no sentido anti-horário, logo:
A curva está no sentido horário, logo:
A curva está no sentido anti-horário, logo:
Finalmente:
A resposta certa é a .
Resposta