Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Ampère

Ver Teoria
Exercício 931234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192949596979899100

Enunciado

Passo 1

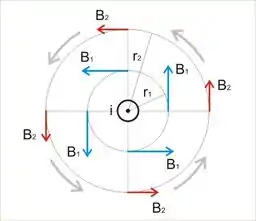
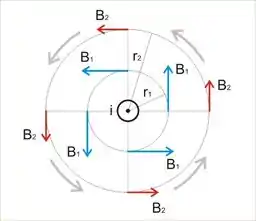
Pela lei de Ampère, campos “girantes” são gerados pelo fio, o sentido desse giro pode ser descoberto pela regra da mão direita e, quanto mais longe do fio, menor é a magnitude desse campo ok? Isso é, qualitativamente, o que a lei de Ampère diz e o que podemos concluir com essa figura. Tudo com simetria radial, com simetria “redonda”.

Passo 2

Se r > R então um círculo imaginário iria envolver toda a corrente i beleza? Por isso, aqui, aplicamos a lei de Ampère assim:

μ 0 . I T O T A L = ( 2 . π . r . B )

A corrente total é dada pela integração dessa densidade de corrente de 0 até R , lembrando que o elemento de área de um círculo é d S = 2 . π . r . d r

Então:

I T O T A L = ∫ r = 0 R 2 . I π .   R 2 . 1 - r 2 R 2 . 2 . π . r . d r = 4 . I   R 2 . ∫ r = 0 R r - r 3 R 2 . d r

I T O T A L = 4 . I   R 2 . r 2 2 0 R - 1 R 2 . r 4 4 0 R = 4 . I R 2 . R 2 2 - R 2 4 = 4 . I R 2 . R 2 4 = I

Então: μ 0 . I = 2 . π . r . B →

B = μ 0 . I 2 . π . r

Passo 3

Na situação em que r < R a integral que fizemos vai parar no meio, antes que calculemos a corrente total do fio. Então vamos ter:

I I N T = 4 . I   R 2 . r 2 2 0 r - 1 R 2 . r 4 4 0 r = 4 . I   R 2 . r 2 2 - r 4 4 . R 2 = I . r 2   R 2 . 2 - r 2 R 2

I I N T = I . r R 2 2 - r R 2

Nesse caso, a lei de Ampère é a mesma, mas a corrente total da equação muda:

μ 0 . I I N T = μ 0 . I . r R 2 2 - r R 2 = B . 2 . π . r → B = μ 0 . I . r R 2 2 - r R 2 2 . π . r

B = μ 0 . I 2 . π . r . r R 2 2 - r R 2

Resposta

Letra (a)

Letra (b)

B = μ 0 . I 2 . π . r

Letra (c)

B = μ 0 . I 2 . π . r . r R 2 2 - r R 2

Exercícios de Livros Relacionados

41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo