Parte I
Em uma determinada região existe uma densidade de corrente uniforme de no sentido positivo do eixo .
Qual é o valor de quando a integral de linha é tomada ao longo do contorno amperiano formado pelos três segmentos de linha reta que conectam, consecutivamente, os ponto , , e , onde ?
Parte II
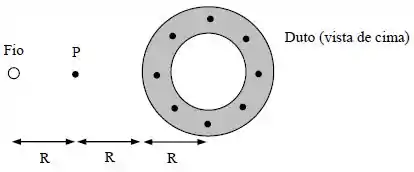
Um duto cilíndrico muito longo, com um raio externo , conduz uma corrente (uniformemente distribuída) (no sentido saindo da página, veja a figura abaixo). Um fio corre paralelo ao duto a uma distância de centro a centro.
Calcule a intensidade (em termo de ), a direção e o sentido da corrente que deve passar no fio para que o campo magnético em seja nulo.
Passo 1
Qual é o valor de quando a integral de linha é tomada ao longo do contorno amperiano formado pelos três segmentos de linha reta que conectam, consecutivamente, os ponto , , e , onde ?
Quando o cara joga essa integral fechada de , a primeira coisa que temos que pensar é na lei de Ampère!
O nosso único trabalho aqui, então, vai ser encontrar o valor da corrente interna .
O problema já falou que a densidade de corrente é uniforme e vale . Ou seja... vamos utilizar isso pra encontrar a corrente que passa por dentro da área formada pelos pontos que, no caso, é esse triângulo aqui em baixo.
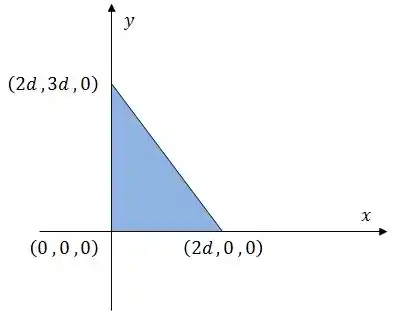
Vamos lá! Pela definição de densidade de corrente, podemos dizer que:
Onde:
Portanto:
Passo 2
Calcule a intensidade (em termo de ), a direção e o sentido da corrente que deve passar no fio para que o campo magnético em seja nulo.
Como a corrente no duto cilíndrico está saindo da página, o campo magnético gerado por ele no ponto estará apontando pra baixo. Assim, o campo magnético gerado pelo fio deve se opor ao campo magnético gerado pelo duto cilíndrico.
Portanto, para que o campo magnético gerado pelo fio esteja apontando para cima, a corrente do fio deve estar no sentido saindo da página.
Os módulos campos magnéticos gerados pelo duto cilíndrico e pelo fio no ponto são dados por:
Para que o campo magnético no ponto seja nulo:
Resposta