Halliday - Vol. 3 – 9º edição – Capítulo 29 – Seção 4 – Exercício 47
(Capítulo 29.4 – Exercício 47) A densidade de corrente no interior de um fio cilíndrico longo de raio é paralela ao eixo central e o módulo varia linearmente com a distância radial de acordo com a equação , em que . Determine o módulo do campo magnético (a) para ; (b) para ; (c) para .
Passo 1
Olá olááá! Bora pra mais uma??
Queremos encontrar o campo magnético para diferentes valores da distância radial em um fio cilíndrico
A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. De acordo com ela:
O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fecahda, conhecida como amperiana. A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:
onde é a densidade de corrente na curva fechada.
Então vamos lá aplicar isso em um fio cilíndrico
Passo 2
Para determinarmos o campo magnético em pontos situados no interior do fio, podemos usar uma amperiana de raio por dentro do fio, conforme a figura abaixo.
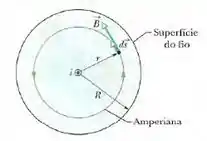
Da lei de Àmpere:
Substituindo :
Agora é só substituir os valores de que foram pedidos
a) Para o , temos o campo magnético igual a zero!
Passo 3
b) Para , temos o seguinte valor para o campo magnético:
Passo 4
c) Para o , temos:
Fechou?
Resposta
- ;
- .