A figura abaixo ilustra um condutor cilíndrico maciço infinito, de raio , que é percorrido por uma dada corrente elétrica constante . Sabe-se que, neste condutor, a densidade de corrente varia com a distância ao eixo do cilindro de acordo com a relação , onde é uma constante positiva e denota a distância ao eixo de simetria do cilindro. A permeabilidade magnética do vácuo é denotada por . Atenção: quando possível, expresse seus resultados em termos de , , e .
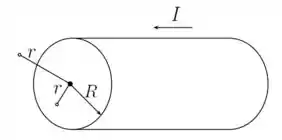
(a) Calcule o módulo do campo magnético no interior do cilindro ().
(b) Calcule o módulo do campo magnético no exterior do cilindro ().
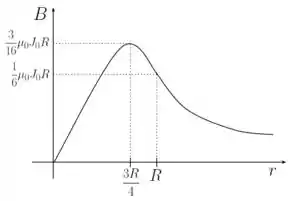
(c) Esboce um gráfico mostrando como o campo magnético varia com a distância ().
Passo 1
Para determinar o campo magnético no interior do cilindro, utilizamos a lei de Ampère no círculo com raio . A corrente que flui através dessa área é:
Passo 2
As linhas de campo magnético, de acordo com a regra da mão direita, são círculos concêntricos com o eixo do cilindro. Além disso, o campo magnético possui o mesmo módulo em todos os pontos do percurso de integração e é tangente à circunferência.
Assim sendo,
Passo 3
Para calcular o módulo do campo magnético no exterior do cilindro, calculamos, inicialmente, a corrente total que passa pelo condutor:
Passo 4
O módulo do campo magnético será, portanto,
Passo 5
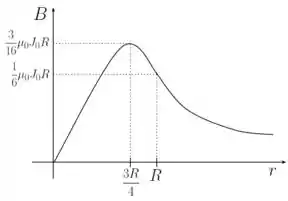
O gráfico pode ser visto abaixo:
Resposta
(a) .
(b) .
(c) O gráfico do módulo de ao longo de é dado por: