Considere quatro condutores cilíndricos, cujas seções retas circulares possuem centros nos vértices de um quadrado, como mostrado na figura abaixo.
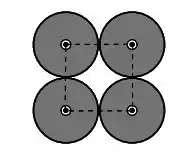
A curva que corresponde a esse quadrado é chamada de . A corrente (uniforme e estacionária) em cada um desses condutores é , e tem o sentido mostrado na figura. Um quinto condutor é colocado na região central limitada pelos quatro condutores, e é percorrido por uma corrente estacionária . Qual deve ser o valor da corrente nesse quinto condutor para que a integral seja igual a zero?
(a)
(b)
(c)
(d)
(e)
Passo 1
Aqui, temos que usar a lei circuital de Ampère, dada por:
Onde corresponde à corrente total que está sendo circulada pela curva .
No caso do problema, a curva está em volta de quartos dos condutores que conduzem uma corrente , o que resulta em uma corrente total circulada igual a .
Desta forma, temos até o momento o seguinte valor de integral: .
Agora queremos colocar um quinto condutor na região central limitada pelos quatro condutores, e esse deve ser percorrido por uma corrente estacionária .
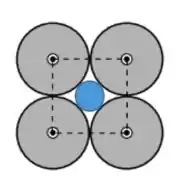
Para que a integral seja nula temos então que adicionar uma corrente de mesmo módulo e sentido contrário, ou seja , justamente para quando somarmos o seu efeito com o que havíamos calculado anteriormente, fiquemos com:
Portanto, gabarito letra A.
Resposta
(a)