A figura abaixo mostra um fio , que consiste de dois segmentos retilíneos, semi-infinitos, ligados a um outro, semicircular, de raio , transportando uma corrente .
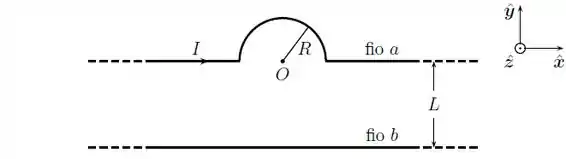
Calcule o vetor campo magnético, gerado pelo fio , no ponto , centro do semicírculo. Justifique cuidadosamente.
Sabendo que um outro fio retilíneo infinito, , está situado a uma distância do fio , paralelo a esse, quais devem ser o valor e o sentido da corrente no fio para que o campo magnético resultante seja nulo em ?
Passo 1
Calcule o vetor campo magnético, gerado pelo fio , no ponto , centro do semicírculo. Justifique cuidadosamente.
Vamos começar dividindo esse cara em 3 partes, duas retilíneas e uma semicircular.
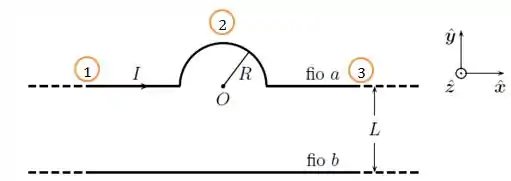
De forma que o campo magnético resultante no ponto será dado por:
O campo magnético gerado por cada uma será dado pela lei de Biot-Savart:
Vamos começar pelos elementos retilíneos.
- Fios 1 e 3:
- Fio 2:
Para esses casos, vamos dar uma olhada nos vetores e , lembrando que tem a mesma direção e sentido da corrente .
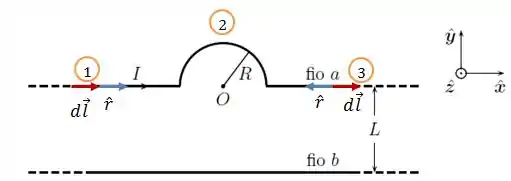
Para ambos os casos, e são colineares, sendo assim:
Portanto:
Passo 2
Novamente, vamos dar uma analisada na situação:
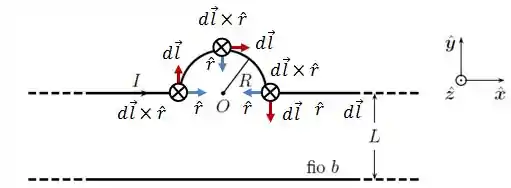
Aqui podemos ver que, para qualquer ponto do fio:
Logo:
Finalmente:
Passo 2
Sabendo que um outro fio retilíneo infinito, , está situado a uma distância do fio , paralelo a esse, quais devem ser o valor e o sentido da corrente no fio para que o campo magnético resultante seja nulo em ?
O módulo do campo magnético gerado pelo fio infinito em um ponto a uma distância é dado pela lei de Ampère:
Para que o campo magnético resultante em seja nulo, o módulo do campo magnético gerado pelo fio deve ser igual ao módulo do campo magnético gerado pelo fio no ponto .
Logo:
O campo magnético gerado pelo fio tem o sentido do vetor . Logo, para que o campo magnético resultante no ponto seja nulo, o campo magnético gerado pelo fio deve ser o sentido do vetor , saindo da página.
Através da regra da mão direita, para que o campo magnético gerado pelo fio tenha o sentido do vetor , a corrente deve estar no sentido positivo do eixo .
Resposta
A corrente deve estar no sentido positivo do eixo .