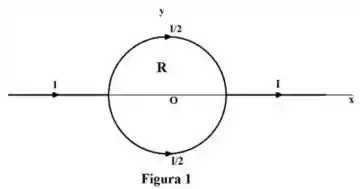
a) Um condutor reto infinito conduzindo uma corrente é dividido em duas partes semicirculares idênticas de raio . Cada parte semicircular conduz a corrente , conforme mostra a Figura 1. Calcule o vetor campo magnético no centro da espira circular assim formada.
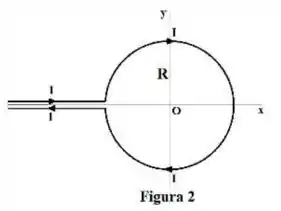
b) Um condutor reto infinito conduzido uma corrente é dobrado conforme mostra a Figura 2. Os fios paralelos semi-infinitos são muito próximos, de modo que suas correntes (opostas) se cancelam mutuamente. Calcule o vetor campo magnético no centro da espira circular assim formada.
c) Calcule o vetor campo magnético devido aos fios semi-infinitos da Figura 1 (que conduzem a corrente ) em um ponto arbitrário do eixo vertical (perpendiculares ao papel) que contém o centro da espira circular. Sugestão: os dois fios semi-infinitos que conduzem a corrente são equivalentes a um fio infinito que conduz a corrente e um fio finito que conduz a corrente .
Passo 1
A primeira coisa de que precisamos nos lembrar aqui é que uma corrente que passa em um comprimento de um condutor, produz um campo magnético em um ponto qualquer do espaço a uma distância de cujo módulo, direção e sentido são dados por:
em que e são vetores que apontam de para o ponto onde queremos calcular o campo magnético . Se quisermos calcular o campo total produzido por todo o condutor percorrido por , temos que integrar a equação acima.
Vamos aplicar isso para o nosso problema...
Passo 2
a) Aqui, é legal a gente separar as seções retas do fio da parte circular para ver a contribuição de cada um. Vamos começar com os fios retos, como na figura abaixo.
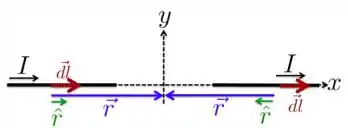
Nessa figura, representamos os vetores , e . Repara que, para o fio que está em , o vetor é paralelo a , portanto, o ângulo entre esses vetores é . Então, o produto vetorial é , o que dá um campo magnético zero. Se fizermos isso para todos elementos desse fio, teremos o mesmo resultado, de modo que o fio todo em não produz campo em .
Agora, para o fio em , é anti-paralelo a , ou seja, o ângulo entre esses vetores é de . Por isso, temos também , resultando também em um campo nulo em . Fazendo isso para todo esse fio, teremos um campo resultante zero.
Passo 3
Já para as partes circulares, é sempre tangente a todos os pontos do condutor e, por isso, sempre perpendicular a . Além disso, todos os elementos estão a mesma distância do ponto , como mostra a figura abaixo.
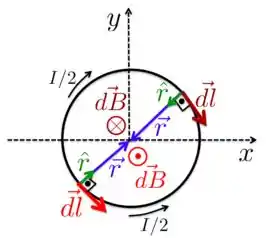
Para todo elemento na parte superior do condutor, existe um outro elemento igual na parte inferior que produz um campo magnético com mesma intensidade, mesma direção, mas com sentido diferente, como mostra a figura: um campo magnético está entrando no plano da página, enquanto o outro, de mesma intensidade, está saindo do plano da página. Por isso, o campo magnético resultante produzido pela parte circular do condutor também é zero!
Então, o campo total resultante devido a ambas as partes retas e circulares do condutor é ZERO!!
Passo 4
b) Neste caso, as correntes que passam na parte superior e na parte inferior da espira circular produzem campos magnéticos ponto que têm a mesmo módulo, direção e sentido. Por isso, o campo resultante será perpendicular ao plano da página, entrando nela.
Falta encontrarmos o módulo desse campo...
Para isso, vamos olhar para o produto vetorial que aparece em . Se a gente aplica a regra da mão direita para esse produto, vamos ter um vetor que está entrando na página e está na direção e sentido de . Portanto,
em que é o ângulo entre e . Bom, para o caso da espira circular:
- e são perpendiculares: ;
- : módulo de um vetor unitário (ou versor);
- : elemento infinitesimal de comprimento;
- : todos os pontos do círculo estão a mesma distância de ;
Vamos pegar essas quatro informações, colocar dentro de e jogar tudo dentro da expressão para do Passo 1 e depois integrar esse cara:
Simplificando essa expressão, temos:
Esse caso a espira circular costuma cair bastante, então vale a pena voltar e ver com cuidado o que a gente discutiu com você, Ok? ;-)
Passo 5
c) Neste item, vamos seguir o que foi na sugestão. O campo magnético resultante no ponto que está sobre o eixo a um distância de pode ser encontrado somando vetorialmente o campo magnético produzido por um fio infinito, cuja corrente está para cima, com o campo produzido produzido por uma corrente que está para baixo em um condutor finito de comprimento , como esquematizado na figura abaixo.
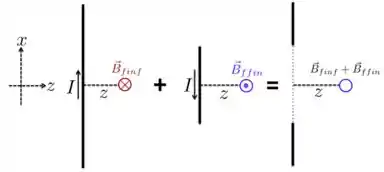
O que precisamos calcular é o campo resultante: .
Campo gerado pelo fio infinito:
Nesse caso, podemos utilizar a lei de Ampère para calcular o campo. As linhas de campo magnético nesse caso são concêntricas ao fio e o campo magnético é tangente a todos os pontos das linhas de campo.
Para isso, vamos tomar como nossa amperiana um círculo de raio orientado de maneira que e sejam paralelos em todos os pontos da curva. Além disso, por causa da simetria do problema, o campo magnético só depende da distância radial ao fio e, por essa razão, tem o mesmo valor em todos os pontos da amperiana.
Colocando isso na lei de Ampère e olhando apenas para a distância , que é a que nos interessa no problema, teremos:
que nos dá um vetor campo magnético no ponto :
Passo 6
c) Continuação...
Campo gerado pelo fio finito:
Para esse caso, vamos usar a figura abaixo.
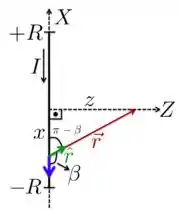
Se utilizamos a regra da mão direita para vetor e fazemos o seu módulo, vemos que:
em é o ângulo entre e , como mostra a figura. Além disso, a gente vê também que os módulos da equação acima são: e . Outra coisa é que, do triângulo retângulo, tiramos que: .
Colocando isso em e depois integrando, chegamos a:
Agora, uma coisa muito importante aqui é que, quando varia na integral acima, o ângulo também varia (dá uma checada lá na figura), o que significa que esse ângulo também depende de . Então, a gente precisa encontrar uma relação entre os dois!!
Da trigonometria, a gente pode usar a seguinte relação entre os ângulos e da figura:
de onde tiramos, olhando para o triângulo retângulo da figura, que:
que é a relação que a gente procurava. Colocando isso em , teremos:
Usando o resultado da integral, que é dado pela prova, temos:
Finalmente (UUUFFAAA...kkk), o campo resultante no ponto será: