Em uma casca cilíndrica de comprimento infinito, raio e coaxial com o eixo passa uma corrente , uniformemente distribuída, que flui no sentido de negativo. No interior desta casca cilíndrica existe uma região cilíndrica (região cinza na figura) também de comprimento infinito, raio e coaxial com o eixo onde há um campo elétrico uniforme , onde é uma constante positiva e é o tempo.
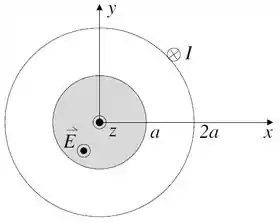
(a) (1,5 ponto) Desconsiderando a casca cilíndrica por onde passa corrente, calcule o vetor campo magnético em todo o espaço (regiões e , onde é a distância ao eixo ).
(b) (1,0 ponto) Determine o vetor campo magnético devido somente à corrente que passa pela casca cilíndrica em todo o espaço.
(c) (1,0 ponto) Calcule o valor da corrente para que o campo magnético seja nulo para .
Passo 1
Para o item (a), vamos utilizar a lei de Ampère incluindo somente a corrente de deslocamento, ou seja,
Passo 2
Pra começar, vamos definir o sentido e direção do campo magnético . Bem, o campo elétrico induz uma corrente de deslocamento com o mesmo sentido e direção de , ou seja, para fora do papel. Dessa forma, pela regra da mão direita, é sempre tangencial às circunferências coaxiais com o eixo (neste caso, de raio ) e possui sentido anti-horário. O vetor está alinhado com . Temos, portanto:
Já o campo elétrico está alinhado com o vetor normal à superfície. Temos, assim:
Como ,
A integral , aqui, irá depender do valor de ! Isso porque estamos apenas interessados na área pela qual passa fluxo elétrico, que é o cilindro cinza de raio .
Assim sendo:
- Se , ; e
- Se , .
Passo 3
Reescrevendo a lei de Ampère para as conclusões acima, chegamos nas soluções abaixo.
- Se :
- Se :
- Se , ; e
- Se , .
Passo 4
Para o item (b), vamos utilizar a lei de Ampère sem o termo de corrente de deslocamento, ou seja,
onde é a corrente de condução ao longo da casca cilíndrica.
Passo 5
O sentido do campo magnético , nesse caso, é o oposto ao campo obtido no item (a), pois agora a corrente está entrando no papel. Dessa forma, pela regra da mão direita, é sempre tangencial às circunferências coaxiais com o eixo (neste caso, de raio ) e possui sentido horário. O vetor está alinhado com . Temos, portanto:
Passo 6
Bem, para , a corrente de condução é aquela que passa pela casca cilíndrica, ou seja, . Assim sendo,
Passo 7
Para , no entanto, a corrente de condução é nula. Nesse caso, portanto, o campo magnético também será nulo!
Passo 8
O campo magnético na região é a soma dos campos magnéticos calculados nos itens (a) e (b). Para que ele se anule, devemos ter, portanto:
Resposta
(a) O módulo do campo magnético para a região é dado por:
O módulo do campo magnético para a região é dado por:
Direção e sentido de são os especificados no Passo 2.
(b) O módulo do campo magnético devido somente à corrente de condução é dado por:
Direção e sentido de são os especificados no Passo 5.
(c) O valor da corrente para que o campo magnético seja nulo para é dado por:
Resposta
Ei, a resposta está no passo a passo :)