Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
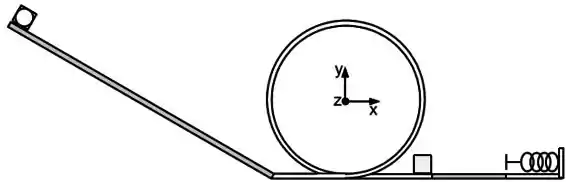
e) Imediatamente antes da colisão, calcule o momento angular , em relação à origem do sistema de coordenadas, do cubo que está em movimento. Suponha a velocidade do cubo imediatamente antes da colisão é de
Passo 1
e)
Podemos utilizar esta fórmula de momento angular:
Entretanto a componente do vetor posição será eliminada por se tratar de um produto vetorial.
Substituindo os dados:
Resposta
e)