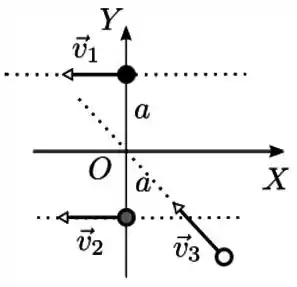
Três partículas de massas iguais a movem-se na ausência de forças externas com velocidades e . Num dado instante elas ocupam as posições indicadas na figura abaixo. O vetor momento angular total deste sistema de partículas em relação a origem do eixo de coordenadas da figura é
(a)
(b)
(c)
(d)
(e)
Passo 1
A gente calcula o momento angular de uma partícula em relação à origem com a fórmula:
seria como o braço da alavanca pro torque, a distância da direção da velocidade da partícula à origem, enquanto é seu momento linear.
O sinal é positivo quando o momento angular faz girar no sentido anti-horário e negativo se ele faz girar no sentido horário.
Passo 2
Vamos começar pela partícula de velocidade .
Ela está a uma distância da origem, e faz girar no sentido anti-horário, então o seu momento angular em relação à origem é:
Passo 3
A partícula de velocidade também está a uma distância da origem, mas ela faz girar no sentido horário, então seu momento angular em relação à origem é:
Passo 4
Vamos finalizar com a partícula de velocidade . Repare que a direção dela aponta diretamente pra origem, então pra essa partícula temos . Logo,
Passo 5
Então o momento angular total desse sistema em relação à origem é dado por:
Resposta
Alternativa (a)
´