Uma partícula se move com velocidade constante . Sobre o momento angular dessa partícula em relação à origem de um determinado sistema de eixos pode-se afirmar que:
(a) O momento angular de uma partícula com velocidade constante sempre é nulo.
(b) Não pode ser nulo em nenhum instante.
(c) Será nulo apenas no instante em que a partícula cruzar um dos eixos cartesianos.
(d) É nulo em todos os instantes se a trajetória da partícula passa pela origem em algum momento.
Passo 1
Calculamos o momento angular de uma partícula por meio de:
Ou seja, o produto vetorial entre o vetor posição da partícula com o vetor momento linear .
Lembrando que o vetor momento linear é um vetor na mesma direção da velocidade :
Passo 2
Vamos considerar dois casos gerais, sendo o primeiro deles onde a trajetória da partícula não passa pela origem:
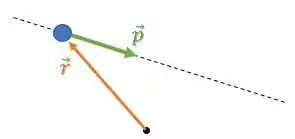
O módulo desse produto vetorial é dado por:
Onde é o ângulo entre eles:
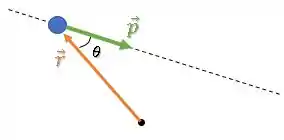
Podemos inclusive escrever esse termo a partir da distância perpendicular do eixo à origem:
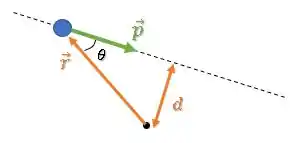
Ficamos então com:
Ou seja, o momento angular será não nulo e ainda por cima constante caso a trajetória da partícula não passe pela origem.
Passo 3
Mas e se a trajetória estiver passando pela origem?

Agora, esse produto vetorial resulta em zero né?
Então, se a trajetória da partícula passa pela origem o momento angular é zero.
Ficamos com a letra (d)
Resposta
Letra (d)