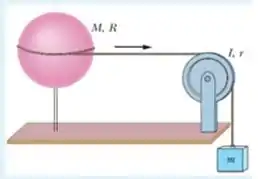
Uma esfera oca uniforme de massa e raio pode girar em torno de um eixo vertical sem atrito conforme a figura abaixo. Uma corda de massa desprezível esta enrolada no equador da esfera, passa por uma polia (um disco homogêneo) de massa e raio , e está presa a um pequeno objeto de massa . Não há atrito no eixo da polia, e a corda não escorrega na casca nem na polia. O sistema é liberado do repouso e o bloco cai de uma altura . No instante final da queda do bloco por essa distância , determine:
- O módulo da velocidade do bloco
- O módulo do momento angular da esfera com relação ao seu eixo de rotação
- O módulo do momento angular da polia com relação ao seu eixo de rotação.
Passo 1
Oi, tudo bem?
O problema diz que não tem dissipação de energia, então vou usar (e abusar um pouco kkk) da conservação de energia!

No começo temos que o sistema está em repouso, então não temos energia cinética (de nenhum tipo! Nem rotacional nem translacional) mas temos energia potencial gravitacional!
A caixa de massa está suspensa por uma altura , então ela tem energia por causa do campo gravitacional da Terra, e é essa energia que, quando o sistema é liberado, vai fazer tudo se movimentar.
Então a energia inicial é:
E a energia final?
Ah! Aí que tá: temos várias energias cinéticas!
A esfera está rodando, então temos energia rotacional dela:
A polia também tá girando, então aqui também temos energia rotacional da polia
E a massa ? Ela não tá girando, mas tá andando! Então temos a energia cinética normal
A ideia é descobrir através da conservação de energia a velocidade do conjunto. E daí encontrar as outras coisas que o problema nos pede.
Tranquilo? Vamos começar?

Passo 2
Vamos agora equacionar essas coisas todas. A energia potencial já sabemos:
A energia cinética do bloco é bem conhecida nossa:
Agora as energias de rotação. Primeiro da esfera:
Aqui o momento de inércia é o momento de inércia da esfera. Consultando numa tabela:
E a velocidade angular pode ser relacionada com a velocidade linear :
Daí: , e na energia de rotação:
Ainda temos que , daí sim temos:
E agora a energia da polia:
A energia de rotação é:
O momento de inércia da polia é o mesmo de um disco de raio e massa . Aí o da polia é:
A velocidade angular da polia pode se relacionar com a velocidade linear do conjunto pelo raio dela :
E a energia de rotação dessa polia é:
Tudo bem até aqui?
Passo 3
Letra (A):
A energia inicial é igual a energia final:
Agora vãos resgatar os resultados do passo anterior:
Podemos cortar as massas e ficamos com uma expressão pra velocidade linear do sistema em termos da altura e da gravidade:
Passo 4
Letra (B):
E agora podemos calcular o momento angular da esfera!
O momento angular é . O momento de inércia de uma esfera de massa e raio é , no nosso caso . Daí temos:
O momento de inércia da esfera:
Mas :
E a velocidade angular:
Aí o momento angular fica assim:
Lembra que já descobrimos a velocidade na letra (a):
Beleza?
Passo 5
Letra (c): agora vamos calcular o momento angular da polia. O momento de inércia de uma polia de massa e raio é . No nosso caso :
E daí o momento angular é:
E a velocidade angular é , então:
Lembra que já descobrimos a velocidade na letra (a):
Juntando os resultados temos:
Beleza?
Espero ter te ajudado! =D