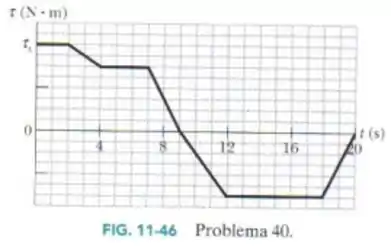
A Fig. 11-46 mostra o torque que age sobre um disco inicialmente estacionário que pode girar em torno do seu centro como um carrossel em função do tempo. Qual é o momento angular do disco em relação ao eixo de rotação nos intantes (a) e (b) ?
Passo 1
Aprendemos que, se temos um gráfico :
Então vamos lá:
Passo 2
- , retângulo de base e altura :
- , trapézio de base maior , base menor e altura 2:
- , retângulo de base e altura :
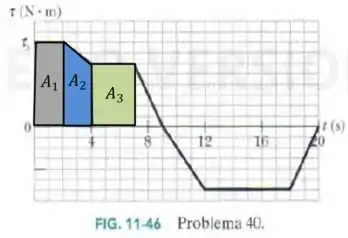
Calculando as áreas, tendo como base que cada quadradinho tem tamanho 1:
Portanto, como o disco está em estado estacionário(), temos:
Passo 3
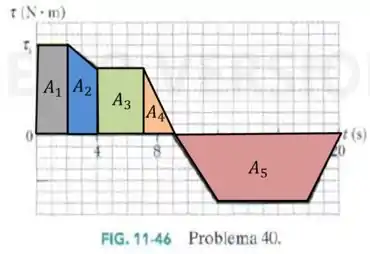
Já calculamos a soma de e , nos resta então calcular as outras duas áreas:
- , área de um triângulo de base e altura .
- , área de um trapézio de base maior , base menor e altura .
E então, lembrando que devemos diminuir a última área, já que está abaixo do eixo, temos: