Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Angular

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Um capacitor de 5,0   μ F é carregado a uma tensão de 30 V e então é ligado a um indutor de 10   μ H . A frequência angular de oscilação das energias armazenadas no campo elétrico do capacitor e no campo magnético do indutor é:

  1. 2,82 × 10 5   r a d / s
  2. 1,41 × 10 5   r a d / s
  3. 7,07 × 10 5   r a d / s
  4. 3,18 × 10 5   r a d / s
  5. 1,41 × 10 5   r a d / s

Passo 1

Pow! Antes de tudo, vamos desenhar esse circuito aí beleza?

Bem, após o capacitor ficar completamente carregado (com a mesma tensão que a fonte), ele se conecta com um indutor:

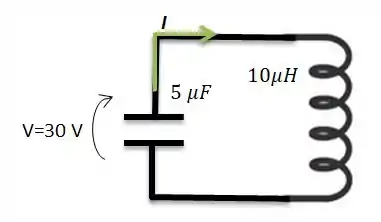
E imediatamente após ele se conectar ao indutor de indutância L = 10   μ H , surge uma corrente para carregar o indutor!

Essa corrente, após carregar o indutor ela volta para o capacitor e assim vai: capacitor indutor... Indutor capacitor. Isso tudo acontece com uma frequência angular ω . O que queremos é justamente esse valor, tai gado?

Passo 2

Cara, então... Podemos calcular essa frequência ω de acordo com a teoria simplesmente se recordando de que em um circuito L C , a frequência presente vai ser a fundamental...

ω = ω 0 = 1 L C

O problema nos deu L = 10   μ H e nos deu C = 5,0   μ F . Como micro significa 10 - 6 ...

ω 0 = 1 10 ⋅ 10 - 6 ⋅ 5 ⋅ 10 - 6     →

ω 0 = 1 50 ⋅ 10 - 12     →

ω 0 = 1 50 ⋅ 10 - 6     →

ω 0 = 1 50   10 6     →

Então...

ω 0 = 0,14 ⋅   10 6 =

1,4 ⋅ 10 5   r a d   / s

Resposta

Letra B

Exercícios de Livros Relacionados

Um bloco homogênea de granito em forma de livro possui faces de 20c m por 15c m e uma espessura de 1,2c m . A massa específica (massa por unidade de volume) do granito é 2,64g / c m 3 . O bloco gira e
10.19E Calcule o momento angular orbital da Terra em termos da constante de Planck.
Um ponto na borda de um rebolo com 0,75m de diâmetro muda de velocidade, a uma taxa constante, de 12m / s para 25m / s em 6,2s . Qual é a aceleração angular média do rebolo?
Em um certo instante, uma partícula de 0,80k g está situada na posição r → = 2,0m i ^ + 3,0m j ^ . O momento linear da partícula está no plano x y e tem um módulo de 2,4k g ∙ m / s e uma direção de 11
Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d