USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 30a
Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .
Calcule o vetor momento angular do sistema e mostre que é o mesmo em relação a qualquer ponto e se conserva.
Passo 1
Eaew, belezinha?
Temos um sistema que pode ser representado como
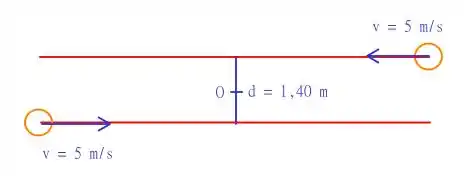
Ambos os patinadores tem e estão se movendo a velocidades , as retas distam de . Precisamos
Calcular o vetor momento angular do sistema e mostre que é o mesmo em relação a qualquer ponto e se conserva.
para proceder vamos usar a definição de momentum angular como
O momentum do sistema será uma soma da forma
note que a escolha arbitrária de um sistema de coordenadas indica que se obtermos uma expressão válida para qualquer vetor posição teremos demonstrado o que está sendo pedido! Saca só!
Passo 2
Note que a todo momento temos que
note também que
isso é válido para a escolha do referencial em uma distância simétrica entre os dois, mas note que a escolha de referencial é arbitrária e isso não irá afetar o resultado! Usando ambas as relações, temos que
escolhendo o momento em que é perpendicular ao momentum linear, temos que
Vamos mostrar que isso se conserva para todo ponto! Saca só!
Passo 3
A conservação do momentum angular é verdade se em um sistema sem forças externas, temos que
derivando em relação ao tempo e usando a regra do produto para a derivação, temos que
como temos que
e como é paralelo à , temos que
e, como a velocidade é constante temos que
Ou seja, podemos garantir que independentemente do valor de temos que
Essa alternativa foi isso! Te vejo na próxima! Até já!