Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Angular

Ver Teoria
Exercício 761234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757778798081828384858687888990919293949596979899100

Enunciado

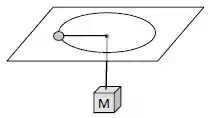
Um corpo de massa m desliza sobre uma superfície horizontal, preso a um fio que passa por um furo. A extremidade do fio está presa a uma massa M . O corpo de massa m gira sem atrito, fazendo uma trajetória raio r i , com velocidade angular suficiente para manter a massa M suspensa. Se a massa suspensa cair para a metade do seu valor inicial, qual a razão entre o raio final e o raio inicial ?

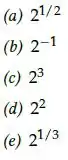
Passo 1

Pra começar sabemos que a força resultante sobre o corpo de massa aponta para o centro do movimento rotacional. Se ela aponta pro centro, ela não exerce torque no movimento, certo ? Então podemos usar conservação de momento angular aqui.

Qual é a ideia? Nós temos duas incógnitas, então precisamos de duas equações, pegou? A primeira vai ser a da conservação do momento angular, a segunda vai sair da relação entre os movimentos. Vem comigo !

Passo 2

Conservando o momento angular temos:

L → i = L → f

m ω i r i 2 = m ω f r f 2

r f r i = ω i ω f

Temos a primeira relação, vamos usar ela ali em baixo !

Passo 3

Usando que a tensão do fio atua como força centrípeta temos:

M g = m ω i 2 r i

M g 2 = m ω f 2 r f

Dividindo uma equação pela outra ficamos com:

ω i ω f = 2 r f r i 1 2

Substituindo o que a gente tinha encontrado la em cima

r f r i 2 = 2 r f r i 1 2

Isolando a razão que a gente quer temos:

r f r i = 2 1 3

Resposta

l e t r a   e )

Exercícios de Livros Relacionados

Um bloco homogênea de granito em forma de livro possui faces de 20c m por 15c m e uma espessura de 1,2c m . A massa específica (massa por unidade de volume) do granito é 2,64g / c m 3 . O bloco gira e
10.19E Calcule o momento angular orbital da Terra em termos da constante de Planck.
Um ponto na borda de um rebolo com 0,75m de diâmetro muda de velocidade, a uma taxa constante, de 12m / s para 25m / s em 6,2s . Qual é a aceleração angular média do rebolo?
Em um certo instante, uma partícula de 0,80k g está situada na posição r → = 2,0m i ^ + 3,0m j ^ . O momento linear da partícula está no plano x y e tem um módulo de 2,4k g ∙ m / s e uma direção de 11
Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d