Um mastro de uma bandeira pode ser modelado por um ahaste homogênea de massa e comprimento que tem presa em sua extremidade uma esfera sólida homogênea de massa e raio . O mastro está preso em sua outra extremidade a uma parede no ponto P, fazendo um ângulo com a horizontal, como ilustra a figura. Utilize g para a aceleração da gravidade.

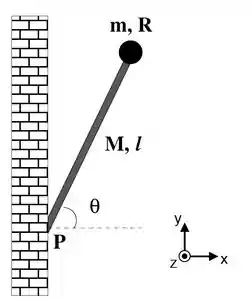
Calcule o momento de inércia rotacional do mastro em torno a um eixo perpendicular ao plano do papel (eixo ) que passe pelo ponto .

Calcule o vetor torque que a força da gravidade faz no mastro em relação ao ponto P.

Suponha que, devido a algum defeito na fixação da esfera, a mesma se solte da extremidade e caia verticalmente. Calcule o momento angular da esfera em relação aoponto P após ela ter caído durante um intervalo de tempo .

Para resolver essa, precisamos lembrar da definição de torque, . Como o mastro é composto por dois corpos, a haste e a esfera, o torque total é a soma dos dois, se liga!

A direção e o sentido do vetor torque foram achados usando a regra da mão direita! Note que o vetor aponta para dentro do papel, e de acordo com o eixo indicado no enunciado, sabemos que deve ser .

Para descobrir qual o momento angular da esfera, vamos primeiro relembrar sua definição, . Como precisamos descobrir o vetor posição da esfera para um tempo , vamos recorrer a boa e velha cinemática. Então vamos achar as componente e separadamente:

Entendeu o porquê tem aquele termo no fim da eaquação para a componente ? Sim...pois a esfera está caindo com a aceleração da gravidade, extamente isso! Agora já temos o vetor !

Agora que temos o vetor posição, falta o vetor momento linear, mas como sabemos, . Ou seja precisamo achar o vetor velocidade, mas a cinemática também responde isso para a gente!

Agora podemos achar o momento angular:

Parece difícil, mas não é! Como temos um produto vetorial, ficamos apenas com: