USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 30b
Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .
Quando os dois patinadores chegam a uma distância um do outro, estendem os braços e dão-se as mãos, passando a girar em torno do centro de massa do sistema. Calcule a velocidade angular.
Passo 1
Eaew, belezinha?
Temos um sistema que pode ser representado como
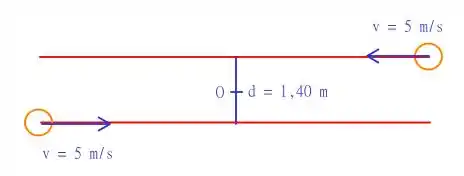
Ambos os patinadores tem e estão se movendo a velocidades , as retas distam de . Precisamos avaliar
Quando os dois patinadores chegam a uma distância um do outro, estendem os braços e dão-se as mãos, passando a girar em torno do centro de massa do sistema. Calcule a velocidade angular.
Para obtermos a velocidade angular podemos usar a relação
E note que quando ambos patinadores dão as mãos não fazem surgir forças externas! Portanto, o momentum angular ainda se conserva! Na alternativa anterior obtivemos que
Vamos obter a nossa velocidade angular! Bora lá!
Passo 2
O problema aqui é simplesmente obter o momentum de inércia do sistema, como temos que cada patinador é um ponto a uma distância de . Podemos escrever o momentum de inércia do sistema como
ou seja, temos que
Ou seja, a velocidade angular temos que
Mais uma alternativa foi! Bora para a última! Vamo que vamo!