USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 40b
40. Uma bola de futebol, de massa e com diâmetro , rola sem deslizar sobre um plano inclinado. Ela parte do repouso e, depois de e tendo completado exatamente rotações, escapa pela borda do plano inclinado. Dado: .
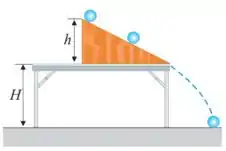
(b) Calcule a energia de rotação da bola ao colidir com o solo
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos uma bola de massa e diâmetro que rola sobre um plano inclinado sem deslizar partindo do repouso e depois de e rotações completas, a bola escapa do plano e cai.
Com isso, queremos saber qual é a energia de rotação da bola quando ela atinge o solo.
Tem ideia de como fazer isso? 😬
Depois da bola cair do plano inclinado, ela está em movimento oblíquo sem ação de forças que podem mudar sua rotação.
Ou seja, a energia cinética de rotação da bola na base do plano inclinado é igual a energia da bola quando ela toca o solo.
Anteriormente calculamos a aceleração angular da bola como
Com essa informação e com as informações dadas no enunciado, podemos descobrir qual é a velocidade angular da bolinha no fim do trajeto e calcular a energia como
Sacou? Bora começar! 😉
Passo 2
Para descobrir a velocidade angular da bolinha, podemos usar a fórmula do movimento rotacional equivalente a ...
A bola parte do repouso, portanto , a aceleração calculamos anteriormente como e por fim o tempo que a bola levou até a base da rampa é .
Substituindo essas informações na equação...
Agora aplicando a fórmula da energia cinética rotacional, temos
O momento de inercia da bola é dada por onde e
Substituindo os valores...
Fim! Iae, o que achou? Responde Aí! 😁
