A figura ,que se refere às Questões 1, 2 e 3, representa um aro que rola sem deslizar sobre uma superfície horizontal.
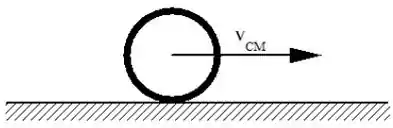
É correto afirmar que o vetor momento angular do aro em relação ao seu centro de massa
(A) aponta para dentro do papel.
(B) aponta para fora do papel.
(C) aponta para a esquerda.
(D) aponta para a direita.
(E) varia de ponto para ponto do aro.
Passo 1
O momento angular de um corpo extenso é dado por:
Ou seja, ele está na mesma direção e sentido que o vetor velocidade angular .
Mas qual é a direção e sentido de .
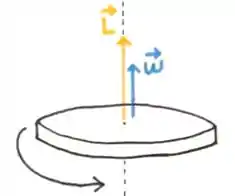
Para isso usamos a regra da mão direita...
Basta você fechar os dedos da sua mão direita no mesmo sentido de rotação do corpo. A direção que o seu dedão estiver apontando será a direção do vetor , e consequentemente também.
Por exemplo:
Então, aplicando a regra da mão direita para o aro, fechamos a nossa mão no plano da tela no sentido horário:
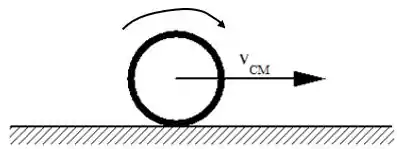
Assim, o nosso dedão está apontando para dentro da tela, certo?
Então esse é o sentido do vetor velocidade angular .
E como:
O nosso vetor momento angular também aponta para dentro da tela.
Ficamos com a letra (A).
Resposta
Letra (A)