Corpos Rígidos, Rotação, Momento Angular
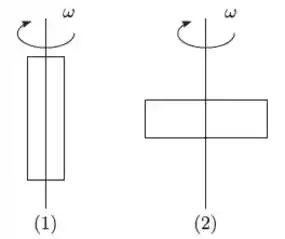
Uma chapa retangular é colocada para girar com velocidade angular constante de duas maneiras diferentes, 1 e 2, como indicado na figura. Nos dois casos os eixos de rotação passam pelos seus centros de massa. As relações entre os módulos dos momentos angulares e , e entre as energias cinéticas de rotação e nas duas situações são
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Os módulos do momento angular e da energia cinética de rotação são dados, respectivamente, por:
Ou seja, pra uma mesma velocidade angular , quanto maior o momento de inércia , maior o momento angular e a energia cinética rotacional.
Então vamos dar uma olhada no momento de inércia da chapa nos 2 casos!
Passo 2
Vamos considerar uma partícula de chapa de massa e distância ao eixo de rotação. Seu momento de inércia em relação ao eixo é:
Ou seja, quanto maior a distância , maior é o momento de inércia da partícula. E de uma maneira geral, o momento de inércia da chapa é:
Então quanto mais massa longe do eixo, mais momento de inércia!
Passo 3
No caso 2 a chapa está atravessada, com uma boa parte longe do eixo, enquanto no caso 1 o lado mais comprido da chapa está paralelo ao eixo, fazendo com que as distâncias entre os pedaços da chapa e o eixo sejam mínimas. Olhando a figura com carinho dá pra ver que no caso 2 tem mais massa longe do eixo.
Portanto, o momento de inércia da chapa é menor no caso 1:
Resposta
Alternativa (b)