USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 31
Um disco com momento de inércia , está girando, com velocidade angular em torno de um eixo sem atrito. Num certo instante, este disco cai sobre outro disco, de momento de inércia , que está inicialmente em repouso, no mesmo eixo. Em virtude do atrito entre as superfícies, os dois discos terminam por atingir uma velocidade angular comum a ambos . Determine . A energia cinética do sistema se conserva?
Passo 1
Oiie, tudo certinho?
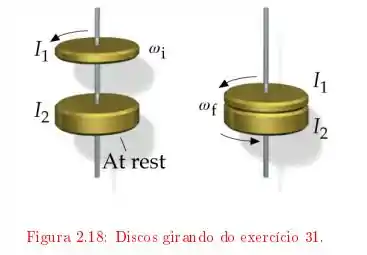
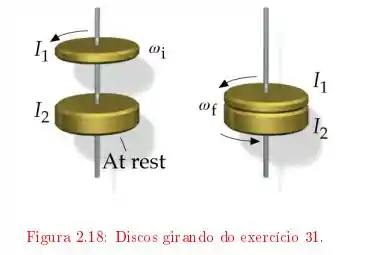
O sistema é tal que temos duas etapas “Antes e depois”, a situação é exemplificada com a figura
Inicialmente temos que o sistema tem um momento angular devido a velocidade angular , dada por
após o sistema se juntar, temos um novo sistema com novo momentum de inércia e nova velocidade angular, mas, o momentum angular deve se conservar já que não há forças externas atuando sobre o sistema! Vamos usar isso para calcular a velocidade angular final! Bora lá!
Passo 2
O momentum angular inicial é dado por
O momentum angular final é tal que
Se desconsiderarmos a espessura dos discos, temos que o momentum de inércia final é dado por
e como temos a conservação do momentum linear, obtemos que
Vamos calcular a energia cinética do sistema! Bora lá!
Passo 3
A energia cinética de rotação é obtida como
O sistema no final é tal que
Usando a velocidade angular obtida no passo anterior, temos que
Como temos que
Portanto, a energia cinética diminui! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e a Energia cinética diminui!