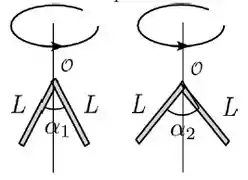
Duas barras finas de mesmos comprimento e massa são dobradas com aberturas de ângulos . Elas são colocadas para girar em torno dos eixos de simetria que passam pelos seus vértices, com mesma velocidade angular constante, como mostra a figura. Sobre sua energia cinética e o módulo do momento angular referido ao eixo de rotação é correto afirmar que:
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
(f) ;
(g) ;
Passo 1
Vamos comparar as energias cinéticas de rotação e os momentos angulares nas duas situações.
Primeiro dá uma olhada nas fórmulas para cada uma dessas grandezas.
Energia cinética de rotação é calculada por:
Enquanto momento angular para um corpo extenso é calculado por:
Bom, a questão já disse que esses dois caras vão girar com a mesma velocidade angular , então, basta nos olharmos para o momento de inércia de cada um deles, que conseguiremos comparar e .
Passo 2
Como temos os dados sobre a geometria da barra, sua massa e sua posição, poderíamos calcular o momento de inércia em cada caso, por mais que isso vá exigir uns conhecimentos de cálculo não tão triviais hahah.

Porém, como só precisamos comparar os dois, uma análise qualitativa já resolve o nosso problema.
Momento de inércia é dado por:
Sendo a distância ao eixo de rotação de cada elemento de massa da barra.
Então, quanto mais afastado do eixo de rotação um elemento de massa estiver, maior será seu momento de inércia.
Dá uma olhada nos dois casos:
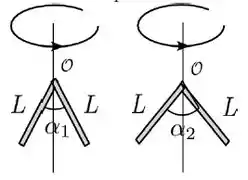
Quanto maior o ângulo de abertura entre as barras, mais afastado do eixo de rotação cada elemento de massa da barra vai ficar. Assim, quanto maior esse ângulo, maior o momento de inércia do conjunto.
Então, o momento de inércia do segundo caso será maior que no primeiro:
Passo 3
Agora ficou mole! Vamos voltar às fórmulas de cada uma das grandezas.
Energia cinética de rotação é:
Então:
Como é o mesmo:
Já o momento angular, é dado por:
Então:
Novamente, como é o mesmo:
Ficamos com a alternativa (a).
Resposta
Letra (a)